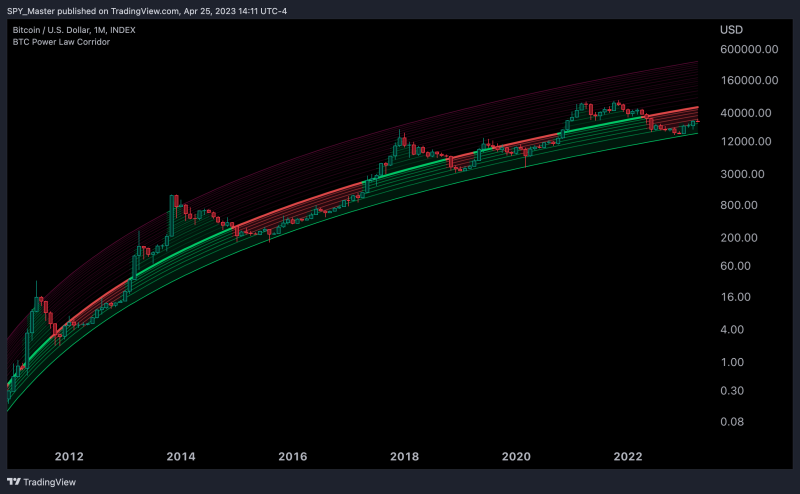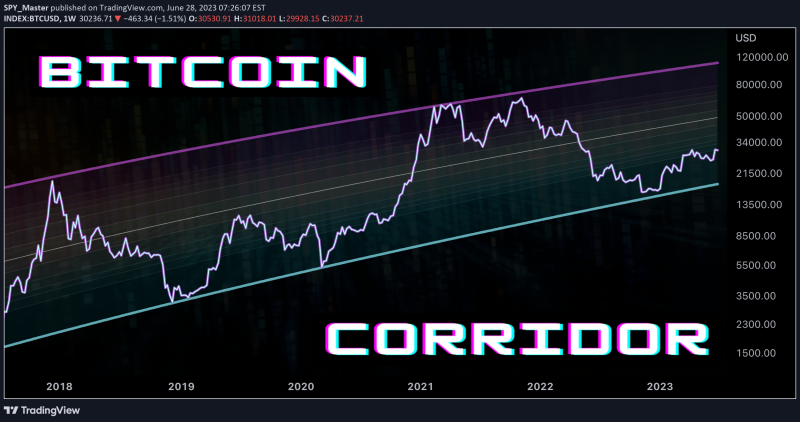
What if there were two straight lines between which all of Bitcoin’s price action could be contained?
If such lines exist, they could provide tremendous insight into the future price of Bitcoin.
As it turns out, the Bitcoin power law corridor theory hypothesizes that such lines may exist. However, in order to see these lines within a price chart, one must dramatically change one’s frame of reference. In this post, I will attempt to change your frame of reference and transform the chart of Bitcoin so that its entire price history is contained between two straight lines.
First, here’s a chart that shows the entire price history of

BTCUSD
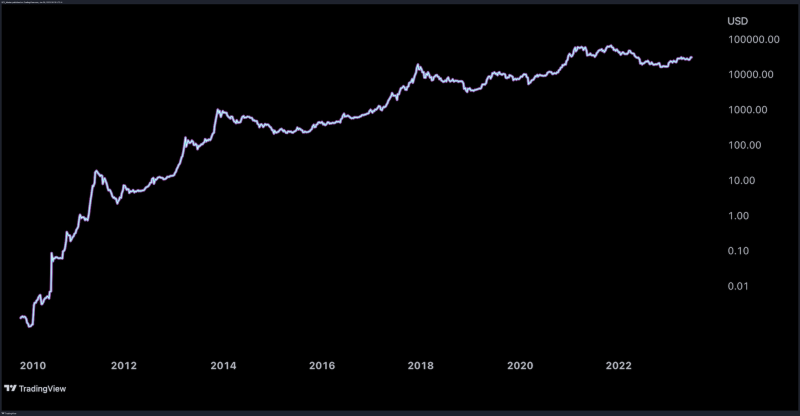
Next, I will log scale the chart. Many users on TradingView know how to log scale their charts, but if you do not, here’s a post on how to do it.
As shown in the chart below, after I log-scaled the chart, I then adjusted the y-axis such that each value on display is a power of 10.
Now, here’s the part where you have to change your frame of reference.
Up until now, you have only seen charts on TradingView with a linear x-axis (time). However, in some cases, it is appropriate to plot time using a logarithmic scale. This is because a logarithmic scale compresses the time dimension, making it easier to see trends over very long periods of time.
Therefore, one can log-scale the time axis of one’s charts to observe the movement of Bitcoin’s price over long periods of time. When this is done, Bitcoin’s price appears to be contained between two straight lines. Bitcoin is bound by these two lines as it oscillates with each halving cycle. As the effects of each halving cycle diminish over time, Bitcoin’s price converges towards a singularity.
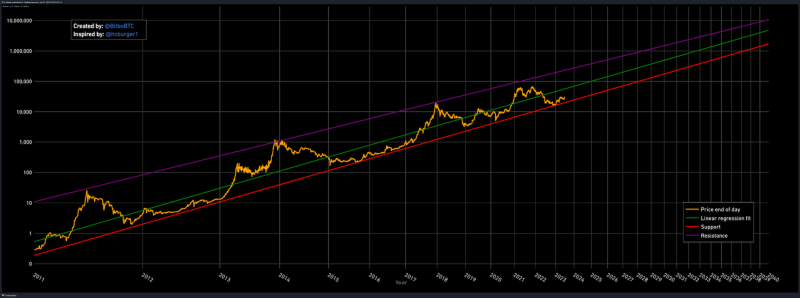
Why does Bitcoin’s price action behave in this manner? The answer is that Bitcoin’s price is an oscillatory logistic growth function. Logistic growth functions approach some finite horizontal asymptote over time. However, when both the horizontal (x-axis) and vertical (y-axis) are logarithmically scaled, the logistic function transforms into a straight line. To read more about the significance of Bitcoin as a logistic growth function, including how it informs my cryptocurrency investment strategy, you can check out my post below.
There are some criticisms of the power law corridor theory, including that Bitcoin’s price data does not sufficiently meet certain assumptions about regression that must be true in order for the theory to also be true. These criticisms are outlined in this article. Additionally, the theory breaks down in the event that the U.S. dollar enters into hyperinflation. In this event, the price of Bitcoin will begin to move up hyperbolically rather than linearly, even on a logarithmic scale. Some argue that rather than moving within a power law corridor, Bitcoin’s price moves according to a hyperbolic growth model. (Watch an animation of this model here). Nonetheless, the power law corridor theory is quite insightful for Bitcoin’s current price action.
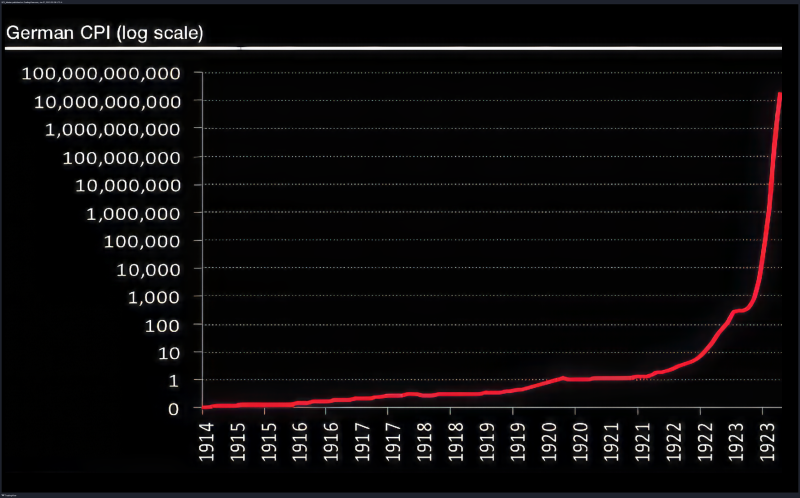
The chart above shows the extreme magnitude of hyperinflation in Germany’s Weimar Republic. For Bitcoin to reach its predicted value under the hyperbolic growth model, the U.S. dollar would need to experience a similar magnitude of hyperinflation during its end stage.
The final thought I want to share may be a bit confusing, but I encourage you to think outside of your usual frame of reference. Here’s a question to get you started: Have you ever noticed that when Bitcoin is plotted as a ratio to any other asset, the chart looks exactly like the price of Bitcoin?
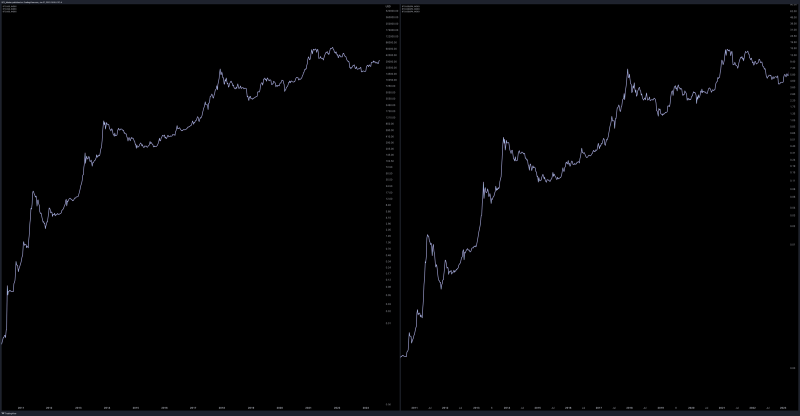
The chart above shows (1) the price action of Bitcoin on the left relative to the U.S. dollar, and (2) shows the price action of Bitcoin relative to the price action of the S&P 500 on the right. Despite being used as a ratio to the S&P 500 in one chart but not the other, both charts still look virtually identical.
With the exception of several other cryptocurrencies, no matter what asset you choose, plotting the entire price history of Bitcoin as a ratio to the asset reveals a logistic growth function. This finding is actually quite significant. It implies that Bitcoin is uniquely suited to become the new standard for measuring value. As an asset with increasingly constant scarcity, Bitcoin is able to achieve what no other financial instrument in history has ever been able to achieve: a constant unit by which the value of all other assets can be measured.
You may not realize it, but virtually all of the charts on TradingView are ratio charts. In most cases, the unit of value measurement is the U.S. dollar. However, since the value of the U.S. dollar changes over time, dependent on the supply of dollars set by the Federal Reserve, the dollar’s ability to be a constant unit for measuring the value of other assets is thus significantly limited.
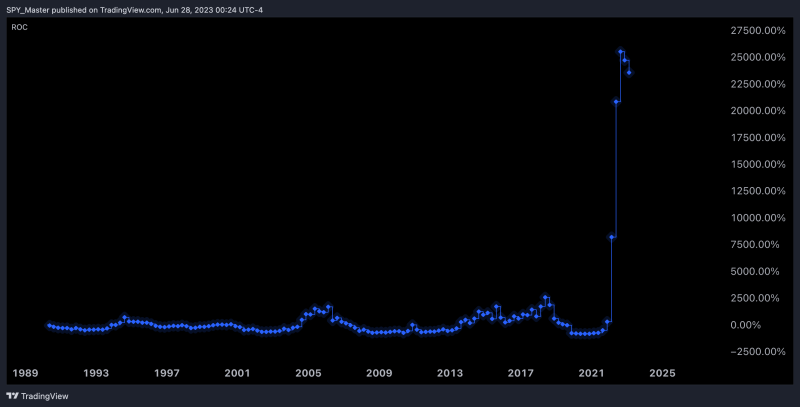
The chart above shows the quarterly rate of change of the 2-year Treasury yield. This yield represents the risk-free rate over a two-year period, which reflects the cost of a U.S. dollar over that period. The volatility of the yield in recent quarters highlights the fact that the value of a U.S. dollar has become unstable. This instability underscores the problem inherent in using the U.S. dollar (or any fiat currency) as a measure of value for other assets.
If Bitcoin indeed becomes an asset by which the value of all other assets is compared, then Bitcoin’s volatility will go to zero because its value will be measured relative to itself. Bitcoin is only volatile right now because its value is being measured in U.S. dollars. Since the value of the U.S. dollar can change widely over time as the central bank expands and contracts the money supply, this volatility in Bitcoin’s price, in large part, actually reflects the volatility in the value of dollars.
In most cases, when an asset becomes the standard for measuring value, is it also considered the risk-free asset. If Bitcoin becomes the risk-free asset, then this fact may upend what Modern Portfolio Theory may consider an optimally efficient, risk-adjusted portfolio. If Bitcoin replaces the risk-free asset, its beta will become equivalent to zero. Suddenly, other cryptocurrencies that outperform Bitcoin, like Ether, may become assets that all efficient risk-adjusted portfolios must contain. This is where my current research ends: The intersection of Bitcoin’s mathematical tendency to replace the risk-free asset and how this could drastically impact the findings of Modern Portfolio Theory and the role played by traditional financial instruments.

It is perhaps no wonder then that traditional financial firms are scrambling to create a spot Bitcoin ETF. Bitcoin represents the next step in the evolution of financial markets. Bitcoin has created the first truly trustless monetary system by solving the Byzantine Generals’ Problem. This problem of trust has plagued financial markets since the advent of credit, and could only previously be temporarily mitigated by increased money creation. However, this fiat approach always ultimately results in hyperinflation and the collapse of the monetary system.
—
Special thank you to @SquishTrade for his editorial assistance. Also, a special tribute to Dr. Harry Markowitz, the father of Modern Portfolio Theory, who sadly passed away as I was researching portfolio theory for this post.
Important Disclaimer
Nothing in this post should be considered financial advice. Trading and investing always involve risks and one should carefully review all such risks before making a trade or investment decision. Do not buy or sell any security based on anything in this post. Past results do not guarantee future returns. Cryptocurrencies are highly volatile. Never borrow money or use margin to invest in cryptocurrency. Cryptocurrency is not backed or insured by any authority and is therefore a high-risk asset class. You can lose all or some of your money in cryptocurrency. Please consult with a financial advisor before making any financial decisions. This post is for educational purposes only. Comment: You can also apply the Bitcoin Power Law Corridor indicator to your chart on TradingView. It’s essentially the same as a Bitcoin Log Growth Curve indicator when time is scaled linearly.